一、前沿
我们在讲解不经意传输(Oblivious Transfer,OT)的文章(安全多方计算(1):不经意传输协议)中提到,利用n选1的不经意传输可以解决百万富翁问题(两位富翁Alice和Bob在不泄露自己真实财富的情况下比对出谁更有钱),过程如图1所示,具体过程不再展开描述。

图1 基于n选1的OT协议实现百万富翁问题
图1中的例子虽然解决了两位富翁在不泄露财富时的比对问题,但是如果遇到其他计算问题(如财富求和)时怎么解决?是否有一种通用的方法,可以在不泄露Alice和Bob原始数据的前提下,实现各种计算问题?本篇文章将向您揭晓答案,即基于混淆电路的MPC通用场景计算。
二、混淆电路简介
我们在安全多方计算系列的首篇文章(安全多方计算之前世今生)中提到,基于混淆电路(Garbled Circuit,GC)可以实现MPC通用场景计算。
2.1 什么是混淆电路
混淆电路是双方进行安全计算的布尔电路。混淆电路将计算电路中的每个门都加密并打乱,确保加密计算的过程中不会对外泄露计算的原始数据和中间数据。双方根据各自的输入依次进行计算,解密方可得到最终的正确结果,但无法得到除了结果以外的其他信息,从而实现双方的安全计算。
2.2 混淆电路执行过程简述
以两方安全计算为例,假设参与方为Alice和Bob,则混淆电路执行过程分为四个步骤:
Step 1: Alice 将计算算法转为混淆电路
Step 2: Alice 和 Bob 进行通信
Step 3: Bob 解密收到的混淆电路
Step 4: 分享结果
每一步的执行细节,将在第三节中以经典的百万富翁问题为例进行详细介绍。
三、基于混淆电路实现安全两方数值比较
百万富翁问题可看作是安全两方的数值比较问题,本节将以数值比较计算方法为例,详述混淆电路执行过程中的四个步骤。
3.1 将数值比较算法转化为混淆电路
3.1.1 画出数值比较算法的逻辑电路
将可计算问题转化为混淆电路的前提,是得到数值比较算法的逻辑电路图。
假设有两个正整数x,y。转换为二进制后,x、y可分别表示为:
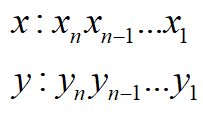
其中xi、yi∈{0,1},当x>y时,x、y的比较过程可简化为:如果最高位xn>yn,直接认定x>y;否则,如果xn-1…x1>yn-1…y1,认定x>y。循环此过程直到最低位。
整个过程中,我们定义一个变量cn+1:
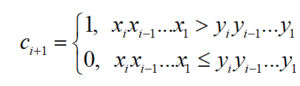
不失一般性,可总结为ci+1=1意味着:(xi>yi)或(xi=yi 并且 ci=1)。这个总结等价于图2中的逻辑电路图:
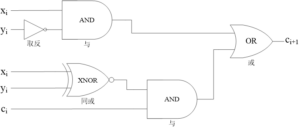
图2 ci+1表达式的等价逻辑电路
则对于正整数x、y来说,将n个图中的逻辑电路进行串联,即可组成完整的数值比较逻辑电路,其中c1=0。完整电路如图3所示。
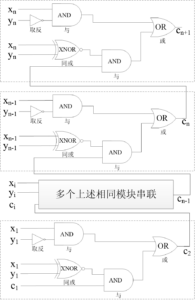
图3 完整的正整数比较逻辑电路图
3.1.2 以最底层模块为例生成混淆电路
(1)写出逻辑电路的真值表
Alice画出可计算问题的逻辑电路后,接下来需要生成整个电路的真值表。我们以整个电路中最下面的模块为例,为了方便理解,我们为每个门电路的输出做上标记,如图4所示。
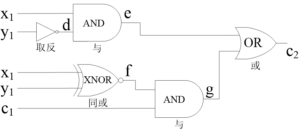
图4 为模块中的所有门电路输出做标记
图4中标记可理解为:输入为x1和y1的“同或门”的输出为f;f与c1是“与门”的输入,该门的输出为g等。图4中模块的门电路真值表如图5所示。
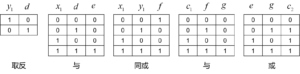
图5 将模块中每一个门电路表示为真值表
(2)以“同或门”为例将真值表转为混淆表
以图5中的“同或门”的真值表为例,讲解如何将真值表转为混淆表。真值表转为混淆表的过程可概括为3个步骤:
第1步:用随机字符串替换真值表中的0和1。
图中的“同或门”一共有3个标签(x1、y1、f),每一个标签有0或1这2个可能的值,因此我们需要用6个随机字符串,来代替3个标签的0\1,这一过程如图6所示。

图6 用随机字符串替换真值表中的0和1
第2步:对替换字符串后的表做加密处理。
加密处理过程如图7所示,加密后的表有4行,每行仅有1个密文数据。图中每一个密文数据均经过两次对称加密而来,其中Ey(f)表示以y为密钥,对明文数据f进行对称加密。

图7 对替换字符串后的表做加密处理
第3步:将加密表的数据排序按行随机置乱。
加密后的表有4行密文数据,如图8所示,将4行密文数据在加密表中所处的行随机置乱。

图8 按行置乱加密表的数据
“将真值表转为混淆表”这一小节中的“字符串替换->加密->置乱”的过程,就是混淆电路的核心思想。
(3)以“同或门”为例对混淆电路进行解密
为了便于读者理解混淆电路的整个执行过程,先以前一小节的“同或门”混淆表为例,讲解另一参与方Bob如何对混淆电路进行解密。前一小节第3步中,Alice已完成了“同或门”混淆表的转换工作,x1表示Alice的输入,y1表示Bob的输入。混淆电路接下来的步骤如图9所示。
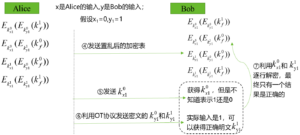
图9 Bob以“同或门”为例对混淆电路进行解密
此过程中,第4~6步展示的是Alice和Bob的通信过程。
第4步:Alice将“同或门”混淆表发送给Bob。
第5步:Alice将自己真是输入所代表的字符串明文发送给Bob,Bob虽然拿到的是明文,但是无法知道该明文字符串表示1还是0。
第6步:Alice与Bob利用不经意传输(OT)协议,将Bob真实输入所表示的两个字符串以密文形式发送,Bob根据实际输入,正确解密获得其中一条明文字符串。
第7步:此时Bob已掌握两条明文字符串。利用这两个明文字符串做密钥,分别尝试解密收到的“同或门”混淆表中的密文,其中仅有一条结果是正确的。
Bob如何知道哪条结果是正确的?Alice对于“同或门”中f标签所表示的0\1明文字符串做加密处理时,可在明文前加128位的0。Bob强行解密完混淆表中的密文后,查看解密结果。如果解密出来的某个消息前面有128个0,就知道此条消息解密是正确的。
最后一步:分享结果。Bob将混淆表中获得的正确消息拿出,Alice拿出f标签所表示的0\1明文字符串映射关系。Alice和Bob即可共同知道“同或门”电路的执行结果。
请注意,混淆电路实际执行过程中,Bob并不会将中间某个门电路的解密结果告诉Alice,仅将整个混淆电路的最终结果告诉Alice。
3.1.3 生成整个逻辑电路的混淆电路
在3.1.1小节画出数值比对算法的逻辑电路后,Alice列出整个逻辑电路中所有门电路真值表,对所有门电路真值表均按3.1.2小节中的“同或门”处理流程转换为混淆电路,Alice可得到整个数值比对算法的混淆电路。
3.2 Alice和Bob进行通信
- Alice将完整的混淆表发送给Bob。
- Alice将每个门电路中,需要用到的xi,每个xi真实输入(0\1)对应的字符串发送给Bob。(实现Alice真实输入值的隐藏)。
- Alice将每个门电路中,需要用到的yi,每个yi所有可能输入(0\1)对应的字符串发,以OT协议形式送给Bob。(OT协议实现Bob真实输入值的隐藏)。
3.3 Bob解密收到的混淆电路
- Bob利用获得的xi、yi、c1,层层强行解密每个相关门电路的输出结果字符串(每个门只能正确解密一个字符串,不给Alice看,实现中间计算结果隐藏)。
- Bob最终可得到整个混淆电路的最终输出结果cn+1所表示的字符串result。
3.4 Alice和Bob共享混淆电路处理结果
Bob将result给Alice看,Alice通过自己掌握的字符串对应表,看真实值0\1。如果为1,表示x>y;否则,表示x≤y。
四、总结
本文讲解了如何通过混淆电路解决百万富翁问题。实际上,计算机所能处理的所有可计算问题都可以转换为逻辑电路,这也就意味着,利用混淆电路可以解决所有的安全多方计算问题:即在混淆电路帮助下,凡是能被逻辑电路表示的计算方法,都能在保证参与方数据机密性的前提下得到正确结果。因此本篇文章将混淆电路称为解决MPC的万能钥匙。
参考文献
[1] https://zhuanlan.zhihu.com/p/138371497
[2] https://zhuanlan.zhihu.com/p/138188677
[3] https://blog.csdn.net/qq_38798147/article/details/110727263
[4] https://blog.csdn.net/Matrix_element/article/details/117481369
版权声明
本站“技术博客”所有内容的版权持有者为绿盟科技集团股份有限公司(“绿盟科技”)。作为分享技术资讯的平台,绿盟科技期待与广大用户互动交流,并欢迎在标明出处(绿盟科技-技术博客)及网址的情形下,全文转发。
上述情形之外的任何使用形式,均需提前向绿盟科技(010-68438880-5462)申请版权授权。如擅自使用,绿盟科技保留追责权利。同时,如因擅自使用博客内容引发法律纠纷,由使用者自行承担全部法律责任,与绿盟科技无关。
