【天枢实验室】模型又不适用了？论安全应用的概念漂移样本检测

阅读： 1,449

引言

机器学习被越来越多地应用到安全场景中，如：恶意邮件检测、入侵检测、WAF等，但是其现实效果饱受诟病，鲁棒性问题往往无法解决，如：A环境下训练的模型换到B环境中不适用，T时刻训练的模型在T1时刻不适用，这导致更换环境时需要标注大量样本，并且模型要定期更新。这种现象在机器学习领域被称之为“概念漂移”，指的是一个模型要去预测的一个目标变量随着时间的推移发生改变的现象，这种现象在安全领域这种高度动态的场景中尤其明显。本文介绍一种检测概念漂移样本、并对结果提供可解释性的方法，该方法来自2021年Usenix Seurity的一篇论文^[1]。

背景

在安全场景下部署机器学习算法的一个重大阻碍就是“概念漂移”现象，只要是在“封闭世界”中学习到的模型，应用到“开放世界”中都会遇到类似的问题，该现象在安全中尤其明显，如恶意软件检测，在封闭训练集上有良好性能的分类器，当输入一个新的家族样本或者变种后，会被分类器强行分到一个已知家族分类中，而显然该样本不属于任何一个分类，类似的情况在入侵检测、WebShell检测、网站指纹等领域同样会出现，出现这种问题的核心是训练数据与测试数据的分布不一致，而所有的机器学习模型都是基于样本的“独立同分布”假设的，这种分布的不一致性往往也是导致机器学习模型不适用的根本原因。

为了克服上述问题，工业界往往通过增加训练集样本，重新训练模型来让模型“看到”更多的样本，甚至通过引入黑白名单的方式来控制误报和漏报，然而该方式往往是治标不治本，新的样本总是在源源不断地出现，会另原有模型不断产生误报和漏报，会引入大量的人力成本进行进一步分析、打标签、更新模型。那么有没有一种方法能有效地识别这种新样本呢？举个例子，当我们训练了一个能够区分正常流量、蚁剑、冰蝎的WebShell分类器，当哥斯拉的流量过来时，能否判断出它不属于这3种流量中的任何一种？该问题即“概念漂移”样本检测问题。

本文介绍一种最新的概念漂移样本检测技术（CADE），CADE在检测出概念漂移样本的同时对结果进行解释，即哪些特征是做出该判断的重要特征。该方法已开源（https://github.com/whyisyoung/CADE）

CADE原理

如图1所示，CADE由两部分构成，概念漂移样本检测模块和解释模块，对于检测模块，核心是距离的定义，该距离用于衡量新样本与已知样本之间的距离，距离越大意味着越有可能是漂移样本，对于解释模块，为了衡量哪些特征最能区分漂移样本和训练数据，同样需要设计一个合适的距离函数进行衡量。我们将分别介绍这两个模块。

图1 CADE原理图

概念漂移样本检测

该模块监控新数据找出其中偏离训练集分布的样本，主要用了一种名为“对比学习”的方法，通过对比学习，可以学习到样本在低维空间的向量表示，用该向量对样本之间的距离进行比较。其原理如图2所示，原始样本的特征是个高维向量，使用这些高维向量无法对样本进行有效区分，对比学习的目的在于通过一种方法学习这些高维向量的低维向量表示，使得得到的低维向量对样本有比较好的区分度。这个模型的训练过程是在训练集数据上进行的，当新数据进来时，若其与任何一个分类的距离都比较远，则认为该样本是漂移样本。

图2 对比学习原理

模型整体设计上使用AutoEncoder的思路，得到低维向量表示，同时通过在目标函数中增加对比误差，使得同一类别的样本之间的距离尽量近，不同类别之间样本的距离尽量远。目标函数的公式如下所示，

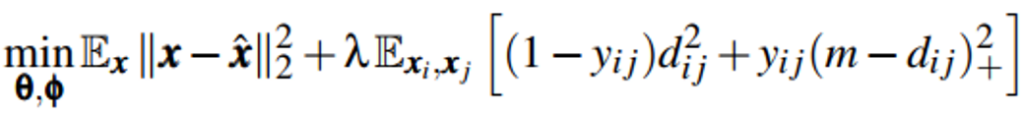
该目标函数由两部分组成，第一部分为基本AutoEncoder损失函数（RMSE，均方根误差）的计算方式，

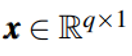
是训练集中的一个样本，维度是q，AutoEncoder模型中，编码器部分表示为f，解码器部分表示为h，其中f的参数为θ，h的参数为∅，编码器将输入向量映射为一个低维向量

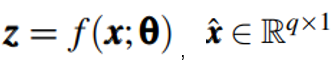
是原始向量的重构向量，解码器的输出，

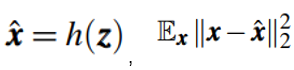
计算的是重构误差。

第二部分为对比误差，其中y_ij为输入样本(x_i, x_j)之间的关系，若两个样本属于同一类，则y_ij=0，否则y_ij=1，(∙)₊是max(0, ∙)的简写，d_ij是两个变量隐空间z_i=f(x_i;θ)和z_j=f(x_j;θ)的欧式距离，该部分的意图在于：若x_i和x_j是同一类别，则最小化两者在隐空间中的距离，若两者属于不同类别，则最大化该距离，上限为m，只要在该半径以内的距离都可以纳入计算范围，设置一个上限m可以保证计算可控，计算结果不受异常点影响，ℷ是控制两者权重的超参。

经过对比学习之后，编码器f可以将样本映射到一个低维空间，在这个低维空间中，同类样本之间距离更紧，不同类之前距离更远（如图2所示），在该隐空间内距离函数可以有效找到偏离这些类的新样本。

解释概念漂移样本

该解释模块旨在识别出概念漂移样本的最重要的几个特征，该问题是深度学习模型的可解释性问题，目前已经有较多的研究工作，该类方法往往通过改变特征值来观察样本的分类是否能够穿越决策边界来确定对应特征的影响力，但是由于样本空间的稀疏性，样本很难穿越决策边界，本文采用基于距离的解释方法，如图3所示，改变特征的目标不是为了穿越决策边界，而是使的样本尽量靠近与最近分类中心的距离，通过这种方式，解释性效果可以大大提高，具体的方法可详见原文^[1]。

图3 基于决策边界和基于距离的解释方法原理

实验结果

作者在文中使用了两个数据集进行了实验，如图4所示一个是恶意软件数据集^[2]，其中包含7个恶意软件家族，共计3000多个样本，另一个是入侵检测数据集^[3]，包含4中类型流量的Flow数据，依据上述方法，在训练时保留一类样本，这类样本用于概念漂移样本的测试，如图5所示，可以看到CADE有比较好的效果，F1值均可以达到0.96，图6对样本的隐空间利用t-SNE可视化出来了，可以看到CADE有非常好的聚类效果，其中在最后一张图中，FakeDoc作为漂移样本，不在训练集当中，可以看到，CADE不仅仅把FakeDoc很好地与其他样本分别出来了，所有的FakeDoc都聚到一个类当中，这也表明CADE不仅仅可以用于检测漂移样本，对样本的聚类也有比较好的效果。

图4 实验数据集，恶意软件数据集Drebin和入侵检测数据集IDS2018

图5 CADE在两个数据上的检测效果

图6 在恶意软件数据集Drebin的T-SNE的可视化效果

结语

机器学习模型在安全应用中总是会因为概念漂移样本而失效，概念漂移样本无法避免，模型换个使用环境，样本进化等因素都会产生概念漂移样本，为了使模型继续发挥效果，概念漂移样本的检测必不可少，基于检测结果，使用者可以对模型的适用情况做出基本判断，有利于标记新样本、模型更新等后续操作，本文介绍了概念漂移样本检测领域的最新研究工作，该方法在两个公开数据集上的F1值都能达到0.96，且提供了可解释性，在任何使用的机器学习的场景中均可使用，有利于对模型进行评估、纠错、更新，该方法值得安全从业者付诸检验、应用。

参考文献：

[1] Yang, Limin, et al. “CADE: Detecting and Explaining Concept Drift Samples for Security Applications.”

[2] Daniel Arp, Michael Spreitzenbarth, Malte Hubner, Hugo Gascon, Konrad Rieck, and CERT Siemens. Drebin: Effective and explainable detection of android malware in your pocket. In Proc. of NDSS, 2014.

[3] Iman Sharafaldin, Arash Habibi Lashkari, and Ali A Ghorbani. Toward generating a new intrusion detection dataset and intrusion traffic characterization. In Prof. of ICISSP, 2018.

【天枢实验室】模型又不适用了？论安全应用的概念漂移样本检测