本文首先介绍量子相关的基本概念、性质及基本原理；接着，从量子通信和量子计算两个部分阐述其原理与发展现状；然后，简单介绍了后量子密码学（也称抗量子密码体制）的发展情况；最后，对量子信息技术的发展进行总结与展望。
1 引言
量子信息科学(Quantum Information)是以量子力学为基础，把量子系统“状态”所带有的物理信息，进行信息编码、计算和传输的全新信息技术。量子信息技术主要包括量子通信和量子计算，由于它们具有潜在的应用价值和重大的科学意义，正引起人们广泛的关注和研究。
本文首先介绍量子相关的基本概念、性质及基本原理；接着，从量子通信和量子计算两个部分阐述其原理与发展现状；然后，简单介绍了后量子密码学（也称抗量子密码体制）的发展情况；最后，对量子信息技术的发展进行总结与展望。
2 量子信息简介
在本章中，首先介绍量子和量子信息基本概念及相关特性；然后介绍量子信息学领域的研究分支及其研究内容。
2.1 量子概念
量子(Quantum)属于一个微观的物理概念。如果一个物理量存在最小的不可分割的基本单位[1]，那么称这个物理量是可量子化的，并把物理量的基本单位称为量子。现代物理中，将微观世界中所有的不可分割的微观粒子（光子、电子、原子等）或其状态等物理量统称为量子。
量子这个概念最早由德国物理学家普朗克在1900年提出的，他假设黑体辐射中的辐射能量是不连续的，只能取能量基本单位的整数倍，这很好地解释了黑体辐射的实验现象。即假设对于一定频率的电磁辐射，物体只以“量子”的方式吸收和发射，每个“量子”的能量可以表示为: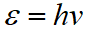
，为普朗克常数。
量子假设的提出有力地冲击了牛顿力学为代表的经典物理学，促进物理学进入微观层面，奠定了现代物理学基础，进入了全新的领域。
2.2 量子基本特性
作为一种微观粒子，量子具有许多特别的基本特性，如量子力学三大基本原理：
- 量子测不准
也称为不确定性原理，即观察者不可能同时知道一个粒子的位置和它的速度，粒子位置的总是以一定的概率存在某一个不同的地方，而对未知状态系统的每一次测量都必将改变系统原来的状态。也就是说，测量后的微粒相比于测量之前，必然会产生变化。
- 量子不可克隆
量子不可克隆原理，即一个未知的量子态不能被完全地克隆。在量子力学中，不存在这样一个物理过程：实现对一个未知量子态的精确复制，使得每个复制态与初始量子态完全相同。
- 量子不可区分
量子不可区分原理，即不可能同时精确测量两个非正交量子态。事实上，由于非正交量子态具有不可区分性，无论采用任何测量方法，测量结果的都会有错误。
除此之外，还包括以下基本特性：
- 量子态叠加性(superposition)
量子状态可以叠加，因此量子信息也是可以叠加的。这是量子计算中的可以实现并行性的重要基础，即可以同时输入和操作个量子比特的叠加态。
- 量子态纠缠性(entanglement)
两个及以上的量子在特定的(温度、磁场)环境下可以处于较稳定的量子纠缠状态，基于这种纠缠，某个粒子的作用将会瞬时地影响另一个粒子。爱因斯坦称其为: “幽灵般的超距作用”。
- 量子态相干性(interference)
量子力学中微观粒子间的相互叠加作用能产生类似经典力学中光的干涉现象。
2.3 量子信息
利用微观粒子状态表示的信息称为量子信息。量子比特(quantum bit或qubit)是量子信息的载体，它有两个可能的状态，一般记为
和
，对应经典信息里的0和1。状态和是二维复向量空间中的单位向量，它们构成了这个向量空间的一组标准正交基。量子比特的状态是用一个叠加态表示的，如
，其中
，而且测量结果为态的概率是
，而得到态的概率是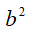
。这说明一个量子比特能够处于既不是又不是的状态上，而是处于和的一个线性组合的所谓中间状态之上。经典信息可表示为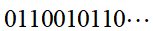
，而量子信息可表示为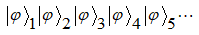
一个经典的二进制存储器只能存一个数：要么存 0，要么存 1。但一个二进制量子存储器却可以同时存储0和1这两个数。两个经典二进制存储器只能存储以下四个数的一个数: 00，01，10 或 11。倘若使用两个二进制量子存储器，则以上四个数可以同时被存储下来。按此规律，推广到N个二进制存储器的情况，理论上，N个量子存储器与N个经典存储器分别能够存储
个数和1个数。由此可见，量子存储器的存储能力是呈指数增长的，它比经典存储器具有更强大的存储数据的能力，尤其是当 N 很大时(如 N=250 )，量子存储器能够存储的数据量比宇宙中所有原子的数目还要多[1]。
2.4 量子信息学
量子信息学是量子力学与信息科学形成的一个交叉学科，该领域主要包括两个领域：量子通信和量子计算。其中量子通信主要研究的是量子介质的信息传递功能进行通信的一种技术，而量子计算则主要研究量子计算机和适合于量子计算机的量子算法。
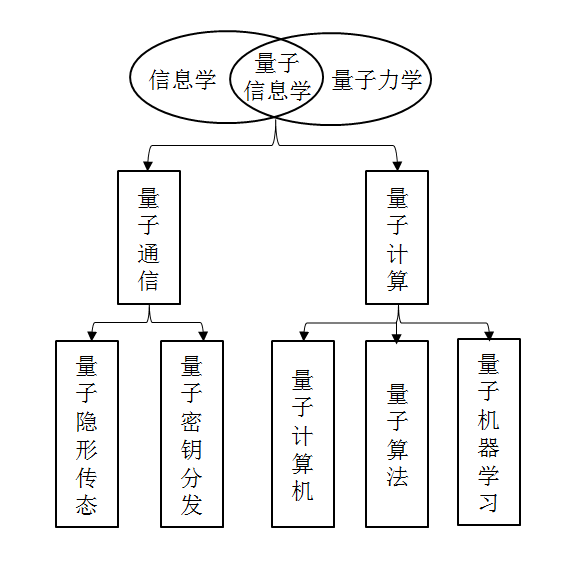
图 1 量子信息学的研究分支
3 量子通信
所谓量子通信，从概念角度来讲就是利用量子介质的信息传递功能进行通信的一种技术。它主要包括量子密钥分配、量子隐形传态等技术。量子密码 (Quantum Cryptography)是利用量子力学属性开发的密码系统。与传统的密码系统不同的是，它的安全性依赖于量子力学属性（不可测量和不可克隆等）而不是数学的复杂度理论。量子密钥分配是研究最为成熟的量子密码技术。在本章中，我们首先简单地介绍量子通信系统的基本模型以及优势，然后介绍量子密钥分配和量子隐形传态的基本原理。接着，概述量子通信的目前研究与发展现状。最后，总结量子通信目前存在的问题。
3.1 量子通信系统基本模型
量子通信体系架构包括量子态发生器、量子通道和量子测量装置以及经典信道等部分，其基本模型如图2所示。
图 2 量子通信系统基本模型
量子通信过程可以从发送端和接收端两个角度理解。
在发送端，量子信源模块产生消息，消息通过量子编码模块转换成量子比特，量子比特通过量子调制模块得到以量子态为载体的量子信息，量子信息通过量子信道进行传输。除此以外，量子调制的模式信息（传统的信息）需要使用经典信道进行传输。
在接收端，将接收到两部分信息：量子信道接收量子信息；经典信道接收额外的经典信息。这两部分信息通过解调和解码模块后，获得最终的消息。
3.2 量子通信技术优势
量子通信与传统通信技术相比，具有如下主要特点和优势：
(1) 时效性高。量子通信的线路时延近乎为零，量子信道的信息效率相对于经典信道量子的信息效率高几十倍，传输速度快。
(2) 抗干扰性能强。量子通信中的信息传输不通过传统信道（如传统移动通信为了使得通信不被干扰，需要约定好频率，而量子通信不需要考虑这些因素），与通信双方之间的传播媒介无关，不受空间环境的影响，具有完好的抗干扰性能。
(3) 保密性能好。根据量子不可克隆定理，量子信息一经检测就会产生不可还原的改变，如果量子信息在传输中途被窃取，接收者必定能发现。
(4) 隐蔽性能好。量子通信没有电磁辐射，第三方无法进行无线监听或探测。
(5) 应用广泛。量子通信与传播媒介无关，传输不会被任何障碍阻隔，量子隐形传态通信还能穿越大气层。因此，量子通信应用广泛，既可在太空中通信，又可在海底通信，还可在光纤等介质中通信。
3.3 量子密钥分配基本原理
量子密钥分配 (Quantum Key Distribution, QKD)以量子态为信息载体，通过量子信道使通信收发双方共享密钥，是密码学与量子力学相结合的产物。QKD 技术在通信中并不传输密文，而是利用量子信道将密钥分配给通信双方，由于量子力学的测不准和量子不可克隆定理，攻击者无法获取正确的密钥。
基于QKD 技术的保密通信系统结构如图3所示，其中上路负责密钥分配，下路负责传输加解密数据。在上路中，量子信道负责传输量子密钥，经典信道负责传输测量基[2]等额外需要的信息。下面，将以BB84[5]方案为例，具体地介绍两条信道起到的作用。
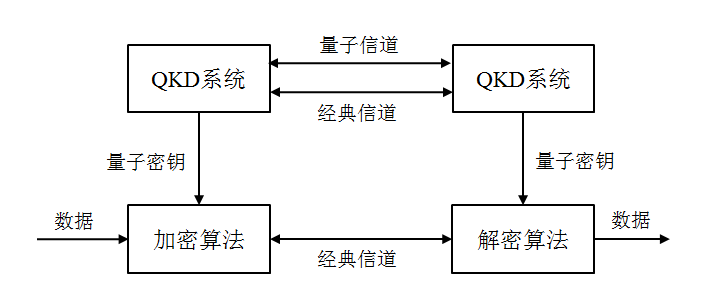
图 3 基于QKD 的量子保密通信系统
BB84 方案。1984 年，Brassard与Bennett联合提出了第一个实用型量子密钥分配系统—BB84 方案，系统架构如图4 所示。
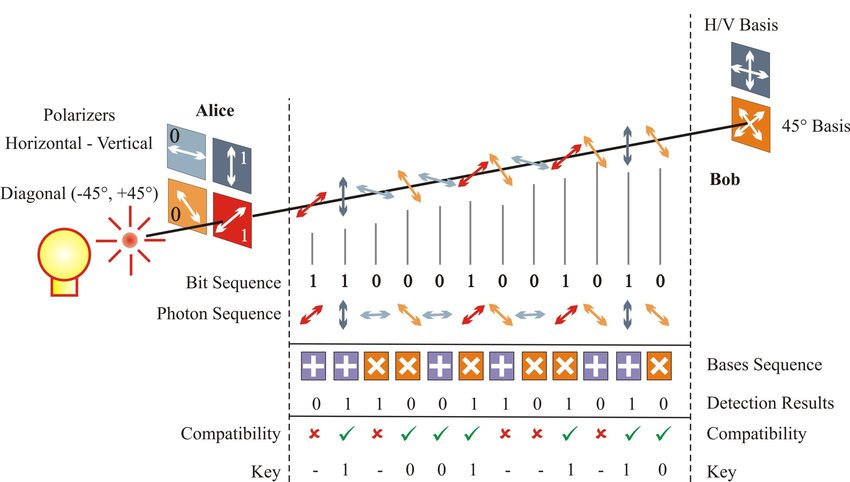
图 4 BB84协议示意图[20]
该方案通过量子信道传送密钥，量子信道的信息载体是单个量子，通过量子的相位、极化方向或频率等物理量携带量子密钥信息。BB84 方案利用单个量子作为信息载体两组共扼基，每组基中的两个极化互相正交。由于理想状态的量子信道无法实现，BB84 方案还利用经典信道进行量子态测量方法的协商和码序列的验证。
假设Alice和Bob使用的是光量子系统，光的偏振态编码为量子信息，不同的偏振态代表量子比特或。如图4，Alice有四种偏振片，水平和垂直方向（组成一组正交基）、－45°和+45°方向（组成一组正交基），因此可以制备四种不同偏振方向的光量子，分别代表、、和。如图4，Bob有两种测量基，第一种可以接收和测量水平或垂直方向的光量子，判断是还是；同理第二种能接收和测量-45°或+45°的光量子，是还是。
有趣的现象：接收端必须使用正确的测量基，才能正确地测出量子比特（光量子的偏振态）；使用错误的测量基，测量结果将发生错误，同时光量子的偏振态发生改变，如图5所示。
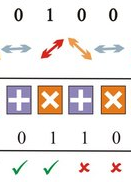
图 5测量基对测量结果的影响[20]
有了以上基础后，理解BB84协议将变得相对容易，其主要步骤如下：
量子信道部分
(1) Alice发送随机的量子比特串给Bob。Alice随机选择四种偏振片，制备不同偏振状态的光量子，得到足够多的随机量子比特并将其发送给Bob。
(2) Bob随机选择测量基测量量子比特。由于Bob并不知道光量子是由发送端那一种测量基编码的，所以他也只能随机选择测量基来进行测量。当选择正确的测量基时，测量的结果正确。当使用错误的测量结果时，测量结果错误。
经典信道部分
(3) Bob将使用的测量基发送给Alice。
(4) Alice将接收的测量基与使用的测量基进行比较，并通过信息告诉Bob哪些位置的测量基是正确的。
(5) Bob根据Alice的消息剔除错误的量子比特，并将选择少部分正确的测量结果告诉Alice。
(6) Alice确认Bob测量结果的正确性。若错误，则说明存在量子信道可能存在窃听，停止通信或者返回第 (1) 步（由于实际的量子信道中也存在噪声，因此会根据一个错误率阈值判断是否窃听和停止通信）。若正确，剔除部分的量子比特，剩下的二进制串作为最终的密钥。并发送确认信息给Bob。
(7) Bob收到确认信息。同样剔除部分的量子比特，剩下的二进制串作为最终的密钥。
我们对BB84协议的安全性做一个简单的分析：
如果Eve在量子信道中旁路窃听，由于量子不可克隆，因此Eve无法复制出一份相同的量子比特副本；如果他在量子信道中直接测量光量子，由于Eve不知正确的测量基，他也会随机选择，有50%的概率选择正确，50%的概率选择错误。若选择的测量基错误，有上述的有趣的现象可知，测量结果错误，同时光量子的偏振态发生改变。当协议的步骤由 (2) 执行到 (6) 时，Alice将发现到量子信道的窃听，那么她将终止这一过程。
如果在经典信道进行窃听呢？实际上也是无效的。即使Eve知道了测量基信息（步骤 (3)），然而由于量子不可克隆，无法得到正确的量子比特串副本。由以上分析可知，BB84协议基于量子不可克隆等原理，实现安全的密钥分配过程。
3.4 量子隐形传态基本原理
量子隐形传态( Quantum Teleportation) 又称量子远程传态或量子离物传态，是利用量子纠缠的不确定特性，将某个量子的未知量子态通过EPR对（纠缠量子对）的一个量子传送到另一个地方（即EPR对中另一个量子），而原来的量子仍留在原处。如图所示6所示，Alice想和Bob通信，具体流程如下：
(1) 制备两个有纠缠的EPR量子（粒子）对，然后将其分开，Alice和Bob各持一个，分别是粒子1和粒子2。
(2) Alice粒子1和某一个未知量子态的粒子3进行联合测量，然后将测量结果通过经典信道传送给接Bob。
此时，神奇的事情发生了：Bob持有的粒子2将随着Alice测量同时发生改变，由一量子态变成新的量子态。这是由于量子纠缠的作用，粒子2和粒子1之间如同有一根无形。
(3) Bob根据接收的息和拥有粒子2做相应幺正变换（一种量子计算变换），根据这些信息，可以重构出粒子3的全貌。
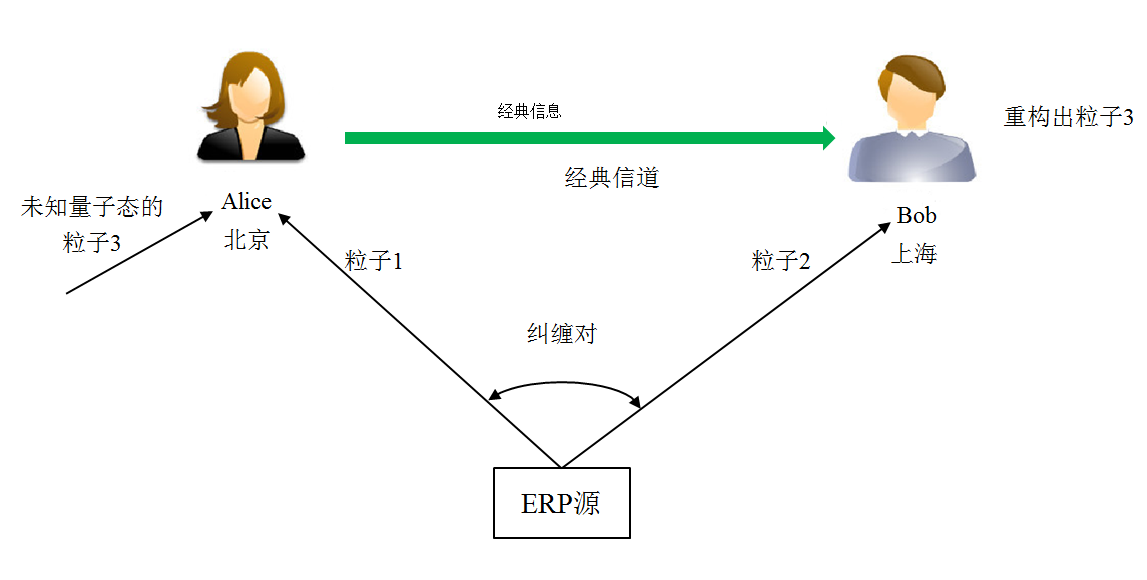
图 6 量子隐形传态原理图
3.5 理论与试验研究进展
1993年，学术界给出了一种利用量子技术传输信息的实际方案，4年后量子通信技术在奥地利科学家的实验室中正式完成了实验验证。经过十多年的发展，量子通信先后实现了信息传递从600m(2007年)到通信距离144km（2012年）的巨大跨越，标志量子通信从理论阶段走向实用化阶段。下面从量子密钥分配和量子隐形传态两个主要研究领域进行介绍。
(1) 量子密钥分配
国外：1993年，英国研究小组首先在光纤中，使用相位编码的方法实现了BB84方案，通信传输距离达10km；1995年，该小组将距离提升到30km。瑞士于1993年用偏振光子实现了BB84方案，光子波长1.3mm，传输距离1.1km，误码率0.54%；1995年，将距离提升到23km，误码率为3.4%；2002年，传输距离达到67km。2000年，美国实现自由空间量子密钥分配通信，传输距离达1.6km。2003年，欧洲研究小组实现自由空间中23km的通信。2008年10月，欧盟开通了8个用户的量子密码网络；同月，日本将量子通信速率提高100倍，20km时通信速率达到1.02Mbit/s，100km时通信速率达到10.1kbit/s。目前，国外光纤量子密钥分配的通信距离达300km，量子密钥协商速率最高试验记录在50km光纤传输中超过1Mb/s[2]。
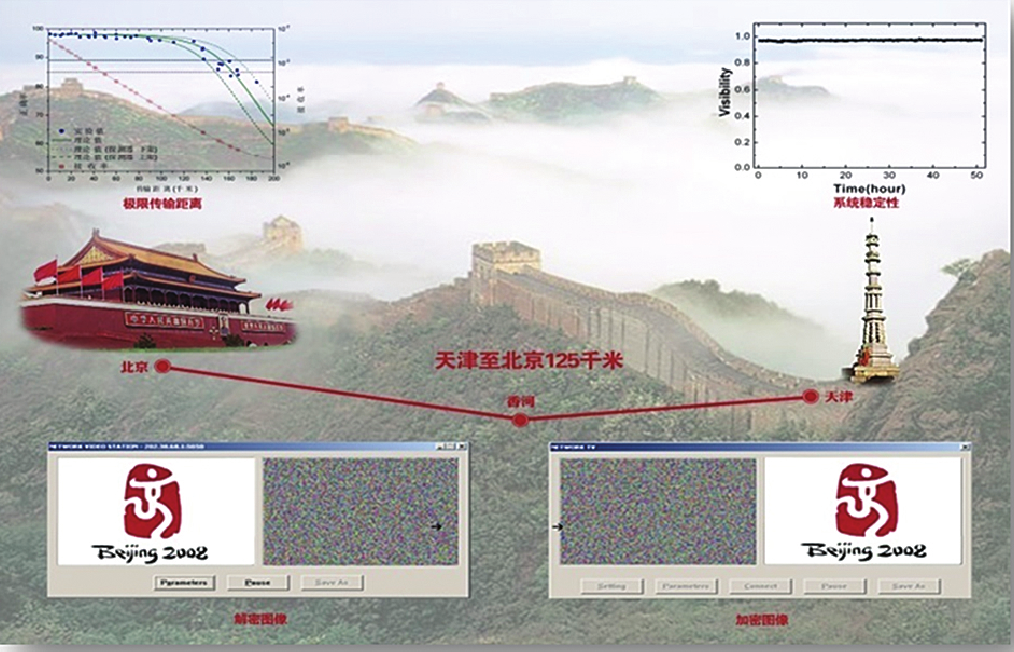
图7 北京—天津量子密码实验[1]
国内：2004年，郭光灿团队完成了途径北京望京—河北香河—天津宝坻的量子密钥分配，距离125km。2008年，潘建伟团队建成基于商用光纤和诱骗态相位编码的3节点量子通信网络，节点间距离达20km，能实现实时网络通话和3方通话。2009年，郭光灿团队建成世界上第一个“量子政务网”。同年9月，中国科技大学建成世界上第一个5节点全通型量子通信网络，实现实时语音量子密码通信。2011年5月，王建宇团队研发出兼容经典激光通信的“星地量子通信系统”，实现了星地之间同时进行量子通信和经典激光通信。2012年2月17日，合肥市城域量子通信实验示范网建成并进入试运行阶段，具有46个节点，光纤长度1700km，通过6个接入交换和集控站，连接40组“量子电话”用户和16组“量子视频”用户。2013年5月，中科院在国际上首次成功实现星地量子密钥分发的全方位地面试验。同年11月，济南量子保密通信试验网建成，包括三个集控站、50个用户节点[2]。在2016年8月16日，我国发射首颗“墨子号”量子卫星，这标志着我国在全球已构建出首个天地一体化广域量子通信网络雏形，为未来实现覆盖全球的量子保密通信网络迈出了新的一步。
(2) 量子隐形传态
1997 年，奥地利Zeilinger小组首次成功实现了量子隐形传态通信； 1998 年初，意大利Rome 小组实现将量子态从纠缠光子对中的一个光子传递到另一个光子上的方案； 同年底，美国CIT 团队实现了连续变量(连续相干光场) 的量子隐形传态，美国学者用核磁共振( NMR) 的方法，实现了核自旋量子态的隐形传送。2001 年，美国Shih Y H 团队在脉冲参量下转换中，利用非线性方法实施Bell 基的测量，完成量子隐形传态。2002年，澳大利亚学者将信息编码的激光束进行了“远距传物”。1997 年，我国潘建伟和荷兰学者波密斯特等人合作，首次实现了未知量子态的远程传输；2004 年，潘建伟小组在国际上首次实现五光子纠缠和终端开放的量子态隐形传输，此后又首次实现6光子、8光子纠缠态； 2011 年，在国际上首次成功实现了百公里量级的自由空间量子隐形传态和纠缠分发，解决了通讯卫星的远距离信息传输问题。2012年9月，奥地利、加拿大、德国和挪威研究人员，实现了长达143公里的“隐形传输”[2]。
3.6 产业化进展与面临的挑战
量子通信的战略意义吸引了西方各国科研机构的关注，IBM、NIST、Battelle、NTT、东芝、西门子等著名公司和机构一直密切关注其发展并投资相关研究。英国政府在2013年发布了为期5年的量子信息技术专项，投入2.7亿英镑用于量子通信和量子计算等方面的研究成果转化，促进新应用和新产业的形成。国外成立了多个专门从事量子通信技术成果转化和商业推广的实体公司。例如美国的MagiQ公司和瑞士日内瓦大学成立的idQuantique公司等，能够提供QKD量子通信的商用化器件、系统和解决方案。法国电信研究院成立的SeQureNet公司从事连续变量量子密钥分发产品的开发。美国洛斯阿拉莫斯国家实验室成立了Qubittek公司，主攻智能电网安全通信领域[4]。
国内开展量子通信相关研究的代表性机构包括中国科学技术大学、中国科学院微系统所和技术物理所、清华大学、山西大学和南京大学等。以中国科学技术大学相关研究团队为核心发起成立了科大国盾量子、安徽问天量子和山东量子等产业化实体，进行量子通信前沿研究成果向应用技术和用化产品的转化，国家对量子通信领域持续的专项投入和政策扶持为其发展提供了强劲动力。
(a) 量子密钥分发机 (b) 量子安全加密手机
图 8 科大国盾量子公司的产品
相比其他量子信息技术，QKD无论在理论中、试验中还是实际应用中，都已经取得了一些重要的进展。然而，大规模的应用和推广仍然面临一系列的困难和挑战[4]，主要表现以下四个方面：
(1) 初期市场规模和用户群体十分有限。量子通信目前主要面向的是有高安全性要求的特定应用场景，如银行、政务和国防等通信网络环境。传统通信业界对于量子通信的应用目前仍然持观望态度，参与度和热情较低。
(2) 产业化供应链的建立尚需时日。QKD 系统采用的单光子源和光子探测器等核心器件与传统光学器件完全不同，生产将面临量子设备特有的器件参数、制造工艺等新的挑战，因此需要一段时间的发展与适应。
(3) 行业标准与规范研尚不完善。对于任何高新技术而言，测试认证和标准化是商用化推广的必备条件，而新型测试认证技术的开发通常是非常复杂、昂贵和耗时的。目前测评技术和标准化研究已经成为量子通信实用化的一大瓶颈。
(4) 基础设施建立目前难以实现。QKD 系统前期需要更多的投入与改造，将原有传统的通信系统升级量子通信系统，将消耗巨额的经济成本。QKD 系统的量子态信号和传统强光信号的混传，所以大规模量子通信组网需要额外的光纤资源进行支持，将对量子通信系统的应用造成限制。此外，量子通信无法共享传统光通信设备等基础设备，需要进行全新部署， 造成前期大量软硬件升级改造的高投入要求。
4 量子计算
量子计算利用量子态的叠加性和纠缠性信息的运算和处理，其最显著优势在于“操作的并行性”，即个叠加态的量子信息进行一次变换，相当于对个量子信息同时进行操作。在本章中，我们将首先介绍三种典型的量子算法的原理，进而介绍量子机器学习与深度学习算法相关知识，最后介绍量子计算机的基本原理和量子编码相关知识。
4.1 典型量子算法
量子算法是量子计算的灵魂。可以说，没有量子算法就无法实现量子计算的并行性。因此，寻找和设计量子算法是量子计算的关键。在量子算法的研究中，出现了三个里程碑式的重要算法：Shor算法，Grove算法和HHL算法，它们都具有较高的理论意义和应用价值。
(1) Shor算法
大整数素因子分解难题指的是：将两个大的质因子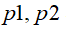
相乘容易，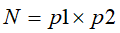
，但将它们相乘的结果分解为两个素因子十分困难。经典算法求解该问题时计算复杂度会随着问题的规模指数增长，目前最有效的传统求解方法复杂度为
，其中表示的位数。众所周知，RSA公钥密码正是基于这样的一个数学难题。
1994年，应用数学家Shor 提出了一个实用的量子算法，通常称为Shor算法[12]。它的出现使得大整数分解问题在量子计算机中在多项式时间内解决成为可能，它计算复杂度仅为
。显然，相比经典算法，Shor算法相当于进行了指数加速。算法主要思想是将整数质因子分解问题转化为求解量子傅里叶变换的周期，将多个输入制备为量子态叠加，进行并行处理和操作，从而到到了量子加速的目的。
在实际应用中， 2001年，IBM公司的研究小组首次在开发的核磁共振（Nuclear magnetic resonance，NMR）量子计算机中使用Shor算法，成功将15分解成3×5，这一成果引起业界广泛的关注和讨论。理论上，一旦更多量子比特的量子计算机研究成功，对于1000位大整数，采用 Shor算法可以在不到1秒内即可进行素因子分解，而采用传统计算机分解需要年（而宇宙的年龄为年）。由此可见在量子计算机面前，现有的公开密钥 RSA体系不再安全。
(2) Grove算法
搜索问题指的是从个未分类的元素中寻找出某个特定的元素。对于该问题，经典算法逐个地进行搜寻，直到找到满足的元素为止，平均需要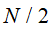
，时间复杂度为
。
1996年，计算机科学家Grover在提出一个量子搜索算法，通常称为Grover算法[13]。采用该量子算法进行搜索仅需次
，复杂度为
。相比传统算法，它进行了二次加速，再次体现了量子计算并行带来的高效优势。举一个直观的例子，若要从有着100万个号码的电话本中找出某个人的号码。经典方法是逐个地进行搜索，平均需要搜索50万次才能找到正确的号码。而采用Grover的量子算法，它会首先将100万个号码制备为量子叠加态[3]。然后在制备的量子叠加态上通过反复执行量子操作的迭代，每一次迭代，它将放大正确的态（寻找的电话号码）的概率，同时减少非正确的态的概率。当进行
次后，正确态的概率接近于1，此时去测量，可以正确态的结果，从而得到查找的电话号码。
由于很多问题都可以看作一个搜索问题，如寻找对称密码(DES/AES等)的正确密钥，搜索方程的最佳参数等，因此Grover算法的用途十分广泛。
(3) HHL算法
求解线性方程是一个基本的数学的问题，在工程等领域有重要的广泛。对于方程，其中A是
的矩阵，是维向量，求解维未知向量。若采用 Gauss 消元法可以在
时间内求解。
2008年，Harrow、Hassidim A和Lloyd S三位学者提出了一种可以在
时间内求解线性方程组的量子算法[14]，通常称为HHL算法。同样地，需要将多个输入制备为量子态叠加，从而进行量子并行操作。
由于机器学习算法中的某些求参过程同样可看作是该类问题，因此学者们已经将 HHL 算法应用到机器学习领域，比如 K-means 聚类,支持向量机，数据拟合等算法中，从而达到加速的目的。
4.2 量子机器学习与深度学习算法
在量子算法中，有一类算法是应用在机器学习或深度学习领域。由于近年来人工智能和机器学习/深度学习的研究热潮，同样带动了量子机器学习/深度学习的发展和研究。
众所周知，传统的机器学习/深度学习算法仍然面临计算瓶颈的挑战。然而，若充分利用量子计算的并行性，则可以进一步优化传统机器学习算法的效率，突破计算瓶颈，加速人工智能进程。量子机器学习的研究可追溯到1995年，Kak最先提出量子神经计算的概念[15]。相继学者们提出了量子聚类、量子深度学习和量子向量机等算法。2015年，潘建伟教授团队在小型光量子计算机上，首次实现了量子机器学习算法[16]。
从经典—量子的二元概念出发可以将机器学习问题按照数据和算法类型的不同分为4类，如表1所示[9]。
表1 机器学习分类
| 简称 | 算法类型 | 数据类型 | 应用实例 |
| C-C | 经典 | 经典 | 传统机器学习 |
| C-Q | 经典 | 量子 | 量子优化控制 |
| Q-C | 量子 | 经典 | 量子支持向量机等 |
| Q-Q | 量子 | 量子 | 量子反馈控制 |
量子机器学习的训练数据必须以某种可以为量子计算机识别的格式载入（即制备量子叠加态），经过量子机器学习算法处理以后形成输出，而此时的输出结果是量子叠加态的，需要经过测量得到最终结果[9]，该流程如图9所示。
图9量子机器学习的基本流程
表2概述了目前文献中见到的一些典型量子机器学习算法，及其所需资源和性能改善特征[9]。
表2 主要量子机器学习算法
| 算法 | Grover
搜索 |
量子加速 | 量子数据 | 泛化
性能 |
实验 |
| K-均值 | 需要 | 平方 | 不需要 | 无 | 无 |
| K-近邻 | 需要 | 平方 | 不需要 | 数值分析 | 无 |
| 主成分分析 | 不需要 | 指数 | 需要 | 无 | 无 |
| 神经网络 | 需要 | — | 不需要 | 数值分析 | 有 |
| 支持向量机1 | 需要 | 平方 | 不需要 | 解析分析 | 无 |
| 支持向量机2 | 不需要 | 指数 | 需要 | 解析 | 有 |
| 回归 | 不需要 | — | 需要 | 无 | 无 |
| Boosting | 不需要 | 平方 | 不需要 | 解析 | 有 |
| 波尔兹曼机 | 不需要 | 量子退火 | 不需要 | 概率生成 | 有 |
如前所述，量子机器学习算法相比经典算法，有以下显著优势：
(1) 量子加速。由于量子态的可叠加性，相比传统计算机，量子算法可以在不增加硬件的基础上实现并行计算，在此基础上利用Shor算法、HHL算法和Grover搜索等算法，可实现相对于完成同样功能的经典算法的二次甚至指数加速[4]。
(2) 节省内存空间。将经典数据通过制备量子态叠加编码为量子数据，并利用量子并行性进行存储，可实现指数级地节省存储硬件需求。
4.3 量子计算机
所谓量子计算机，它是指具有量子计算能力的物理设备。为什么要出现这种设备呢？主要有两个原因：(1) 外部原因：摩尔定律失效。根据摩尔定律，集成电路上可容纳的晶体管数目每隔24个月增加一倍，性能也相应增加一倍。然而，一方面随着芯片元件集成度的提高会导致单位体积内散热增加，由于材料散热速度有限，就会出现计算速度上限，产生“热耗效应”。另一方面元件尺寸的不断缩小，在纳米甚至埃尺度下经典世界的物理规律不再适用，出现“尺寸效应”。(2) 内部原因：量子计算机的强并行性。这是量子计算机相比传统计算机的显著优势，量子计算机和量子算法相互结合，可以将计算效率进行二倍加速甚至指数加速，例如传统计算机计算需要1年的任务，使用量子计算机可能需要不足1秒的时间。
不同于传统计算机，量子计算机用来存储数据的对象是量子比特；不同于传统计算机，量子计算机用使用量子逻辑门进行信息操作，如对单个量子操作的逻辑门：泡利-X门，泡利-Y门，泡利-Z门和Hadamard门等；对两个量子操作的双量子逻辑门：受控非门CNOT，受控互换门SWAP等等。
这些量子的逻辑门的操作可以看做一种矩阵变换，即乘以幺正矩阵（可看做正交矩阵从实数域推广到复数域）的过程。图10以Hadamard门为例，表述了对量子态
的形象操作过程。
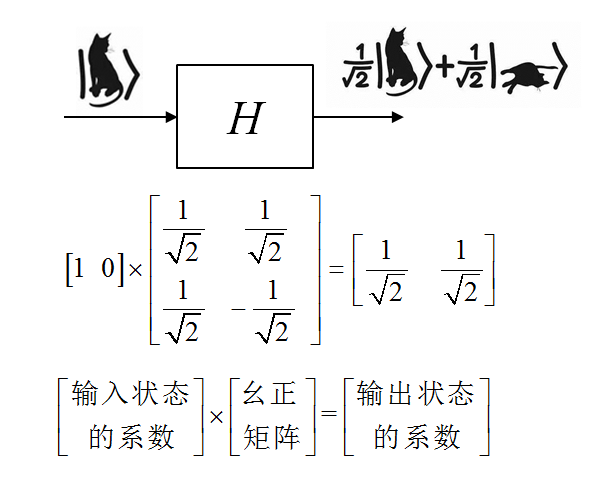
图 10 量子门的操作示意图
由图可知，Hadamard门可以将一个量子态变成两个量子态的叠加状态。形象地说，猫生的状态通过Hadamard门转换成生和死的叠加态（概率为状态幅度的平方，概率各为50%）。这种性质十分有用，是实现并行计算基础，可以将N个输入数据转换成一个叠加的量子态，一次量子计算操作，相当于进行了N个数据操作，即实现了N次的并行，后文提到的量子算法正是利用这些量子逻辑门的变换特性。其他量子逻辑门的幺正矩阵有所不同，但操作也类似，这里不做赘述。
此外，量子计算机用使用的量子逻辑门是可逆的；而传统计算机的逻辑门一般是不可逆的。前者操作后产生的能量耗散，而后者进行幺正矩阵变换可实现可逆计算，它几乎不会产生额外的热量，从而解决能耗上的问题。与传统的计算机相同的是，量子计算机的理论模型仍然是图灵机。不同的是，量子计算目前并没有操作系统，代替用量子算法进行控制，这决定了目前的量子计算机并不是通用的计算机，而属于某种量子算法的专用计算机。量子计算机和传统计算机的比较结果如表3所示。
表3 量子计算机VS 传统计算机
| 属性 | 传统计算机 | 量子计算机 |
| 信息 | 逻辑比特 | 量子比特 |
| 门电路 | 逻辑门 | 量子逻辑门 |
| 基本操作 | 与或非 | 幺正操作 |
| 计算可逆性 | 不可逆计算 | 可逆计算 |
| 管理控制程序 | 操作系统Windows、Linux和Mac等 | 量子算法 |
| 计算可逆性 | 不可逆计算 | 可逆计算 |
| 计算模型 | 图灵机 | 量子图灵机 |
量子计算机的基本原理如图11所示。它主要的过程如下：
(1) 选择合适的量子算法，将待解决问题编程为适应量子计算的问题。
(2) 将输入的经典数据制备为量子叠加态。
(3) 在量子计算机中，通过量子算法的操作步骤，将输入的量子态进行多次幺正操作，最终得到量子末态。
(4) 对量子末态进行特殊的测量，得到经典的输出结果。
图 11 量子计算机工作原理流程图[20]
迄今为止，科学家用来尝试实现量子计算机的硬件系统有许多种，包括液态核磁共振、离子阱、线性光学、超导、半导体量子点等。其中，超导和半导体量子点由于可集乘度高，容错性好等优点，目前被认为是实现量子计算机的两种可能方案[1]。最近，IBM宣布的研制50比特和谷歌研制的72比特量子计算机都是基于低温超导系统的方案。
4.4 量子编码
理论上，需要极少的量子比特便可在量子计算机中实现复杂的量子计算。然而现实中，一方面量子信道上和量子设备中总存在各种噪声，如量子比特的热量等；另一方面量子的“退相干性”[5]。在量子计算，需要使得所有的量子位都持续处于一种“相干态”，然而在现实中很难做到，目前“相干态”仅能维持几百毫秒，随着量子比特的数量以及与环境相互作用的可能性增加，这个挑战将变得越来越大。这两个因素都能导致量子比特的状态翻转或随机化，导致从而导致量子计算失败。量子编码的目的正是为了纠正或防止这些量子比特发生的错误。
虽然量子编码和经典编码的基本想法类似，即要以合适的方式引进信息冗余，以提高信息的抗干扰能力，但量子码可不是经典码的简单推广。在在量子情况下，编码存在着一些基本困难，表现在如下3方面[7]：
(1) 经典编码中，为引入信息冗余，需要将一个比特复制多个比特。但在量子力学中，量子态不可克隆。
(2) 经典编码在纠错时，需要进行测量，以确定错误图样。在量子情况下，测量会引起态坍缩，从而破坏量子相干性。
(3) 经典码中的错误只有一种，即0，1之间的跃迁。而量子错误的自由度要大得多，对于一个确定的输入态，其输出态可以是二维空间中的任意态。
量子编码按其原理，可分为量子纠错码、量子防错码、和量子避错码，其中量子纠错码是经典纠错码的量子推广。在各种量子纠错方案，实际上都假设了发生错误的量子比特数是给定的，例如常见的有纠一位错的量子码。典型的方案是Shor首次给出了一个新颖的纠错编码技术[17]，利用9个量子比特来编码一个量子比特信息，可以纠正一位比特错误。
5 后量子密码
量子计算的快速发展，对当前广泛成熟使用的经典密码算法，特别是公钥密码算法（如RSA和ECC等）产生了极大的威胁和挑战，具体包括[11]：
(1) 所有基于整数分解和离散对数上的非对称密码体制都是不安全的。如RSA、EEC公钥密码算法，它们在多项式时间内可以破解。那么当前主流的公钥加密、数字签名算法将不再安全。
(2) 分组密码和序列密码的比特安全性将降低为原来密钥长度的1/2。为了抵抗这种攻击，对称加密算法通过增加密钥长度（2倍密钥长度）即可。
(3) Hash 算法比特安全性将降低为原来的2/3。
为了抵抗量子计算的攻击，人们提出抗量子密码体制，也称为后量子密码体制(Post-Quantum Cryptography)，即在量子计算机出现之后仍然安全的密码体制。它主要包含基于 Hash的密码体制、基于编码的密码体制、基于格的密码体制和基于多变量的密码体制。事实上，从上述的影响结果来看，目前量子计算仅对公钥密码影响最大，而对分组密码、序列密码、哈希算法相对影响较小，因此可以看作它们也具有一定的抗量子计算攻击的特性。
表3 抗量子密码体制及其具体算法
| 类型 | 典型具体算法 |
| 基于 Hash的密码体制 | Merkle-hash 树签名体制 |
| 基于编码的密码体制 | McEliece算法 |
| 基于格的密码体制 | 格密码算法 |
| 基于多变量的密码体制 | MPKC算法 |
目前，美国和欧洲正在大力对其投入研究，并快速推动其实用化。2015 年8月，美国国家安全局 NSA 宣布将当前美国政府所使用的“密码算法 B 套件”进行安全性升级，用于2015年至抗量子密码算法标准正式发布的空窗期，并最终过渡到抗量子密码算法。2016 年秋到2017年11月，NIST面向全球征集抗量子密码算法，然后进行 3~5年的密码分析工作，预计在 2022年到2023年，完成抗量子密码标准算法起草并发布。
6 总结
量子信息技术主要包含量子通信和量子计算两个分支，本文分别介绍了这两个分支技术。
从理论角度的看，可用数学证明QKD能达到“绝对安全”。然而实践中由于设备和技术的缺陷，QKD不可能达到理想的“绝对安全”，离完全实用化进程还有很长的路需要探索。对此持既批判吹捧量子密码替代传统密码的极端观点，也看好未来量子密码的发展前景。从目前技术成熟度来看，量子密钥分配 ( QKD ) 是最为成熟的量子技术，它结合对称加密技术形成安全的保密通信系统，目前已经实现了商用化，但主要面向政务、国防、金融等安全性要求很高的特定应用场景，离全面推广和实用化还有很长的距离。
从工业界研究热度来看，多数IT和互联网公司致力于研究量子计算，提出“量子计算+人工智能”，以解决计算力瓶颈问题。它具有广泛的应用价值，值得持续关注。
从影响程度来看，量子计算的发展对以RSA和ECC为代表公钥密码学产生了巨大威胁，但对对称加密算法（如AES）的威胁较少。可预见将来，即使量子计算机被研发出来，传统密码也不会完全被替代，而将出现传统密码与量子密码（QKD）相互促进、共同繁荣的景象。
从我国发展状况来看，量子通信技术发展速度迅猛，在理论研究和实验技术上均取得了许多重大突破，成果卓越。然而，量子算法、量子计算机的研究与欧美发达国家相比，仍有很大的差距，相关研究仍需努力。
限于本人知识能力有限，难免出现疏忽与错误，如果您认为存在内容或观点的错误，欢迎您及时指出与交流。笔者十分关注量子计算、量子密码的最新进展以及它们对信息安全行业的影响。如果您也对量子信息技术感兴趣，欢迎与我联系与交流，交流邮箱：chenlei5#nsfocus.com（#号换成@）。
参考文献
[1] 郭光灿，张昊，王琴. 量子信息技术发展概况[J]. 南京邮电大学学报(自然科学版)， 2017， 37(3):1-14.
[2] 徐兵杰，刘文林，毛钧庆，等. 量子通信技术发展现状及面临的问题研究[J]. 通信技术， 2014(5):463-468.
[3] 王矿岩. 量子通信技术发展现状及面临的问题研究[J]. 通讯世界， 2017(1):110-111.
[4] 赖俊森，吴冰冰，汤瑞，等. 量子通信应用现状及发展分析[J]. 电信科学， 2016， 32(3):123-129.
[5] Bennett C H, Brassard G. Quantum cryptography: Public key distribution and coin tossing[J]. Theoretical Computer Science, 2014, 560:7-11.
[6] 陈锦俊, 吴令安, 范桁. 量子保密通讯及经典密码[J]. 物理, 2017, 46(3):137-144.
[7] 段路明， 郭光灿. 量子信息讲座 第三讲 量子编码[J]. 物理， 1998(8):496-499.
[8] 韩永建. 量子计算原理及研究进展[J]. 科技导报， 2017， 35(23):70-75.
[9] 陆思聪， 郑昱， 王晓霆，等. 量子机器学习[J]. 控制理论与应用， 2017(11).
[10] 黄一鸣， 雷航， 李晓瑜. 量子机器学习算法综述[J]. 计算机学报， 2018(1).
[11] 刘文瑞. 抗量子计算攻击密码体制发展分析[J]. 通信技术， 2017， 50(5): 1054-1059.
[12] Shor P W. Algorithms for quantum computation: Discrete logarithms and factoring [C]// Proceedings of the 35th Annual IEEE Symposium on the Foundations of Computer Science. Piscataway, NJ: IEEE, 1994:124-134.
[13] Grover L K. A fast quantum mechanical algorithm for database search[C]// Twenty-Eighth ACM Symposium on Theory of Computing. ACM, 1996:212-219.
[14] Harrow A W, Hassidim A, Lloyd S. Quantum algorithm for linear systems of equations. Phys Rev Lett, 2009, 103:150502.
[15] Kak S. On quantum neural computing[J]. Systems Control & Information, 1995, 52(3-4):143-160.
[16] Su Z E, Wang X L, Lu C Y, et al. Entanglement-based machine learning on aquantum computer[J]. Physical Review Letters, 2015, 114(11):110504.
[17] Shor P W. Scheme for reducing decoherence in quantum computer memory[J]. Physical Review A, 1995, 52(4):R2493.
[18] 孙晓明. 量子计算若干前沿问题综述[J]. 中国科学:信息科学, 2016, 46(8):982.
[19] 赵红敏. 量子纠错与经典纠错的比较[J]. 河北科技大学学报, 2008, 29(3):211-213.
[20] Makarov V. Quantum cryptography and quantum cryptanalysis [D]. 2007.
[1] 这里“不可分割”的含义应该这样理解，比如不可能分割出0.5个原子。
[2]如图4所示，测量基对应为两种不同的偏振片，每个偏振片有两个正交的方向。当偏振片方向可以通过偏振片时，测量结果正确。当偏振片方向不是偏振片的方向，无法通过偏振片，测量结果错误。
[3]由2.3节可知，20个量子比特可同时存储100万个号码。
[4] 表示计算复杂度从降为。
[5]通俗地讲，两束频率完全相同的光源产生相干的量子，它们是相互关联的，即对一个量子进行处理，影响就会立即传送到另一个量子，它们是量子并行处理的基础。但由于外部环境的原因，量子由“相干态”退化为“非相干态”，操作一个量子不会影响另一个量子，它们之间是独立的（类似经典计算机的比特），这就是所谓的“退相干性”。