一、引言
区块链技术最初给我们第一印象是其拥有匿名性,不可篡改性,一致性,分布式等特点。其中匿名性随着对区块链的进一步分析和一些信息情报的收集,一般区块链公链的匿名性都是较弱的。我们熟悉的比特币,以太坊等区块链的匿名性都是较弱的,可以实现交易追踪和地址的聚类,我们在区块链追踪这边也做了一些基础的工作,实现区块链的威胁情报与监管。但是可以通过密码学技术进一步增强区块链的匿名性,其中主流的方法有两种,一种是采用混币的方式其中最具代表性的公链技术是门罗币,这个技术我们在上一篇《区块链隐私保护技术解析——之门罗币(monero)》中进行了详细的分析;另一种技术是采用零知识证明的方式实现强匿名性具有代表性的公链技术是大零币ZEC(Zerocash)。
区块链的交易采用强匿名性是一把双刃剑,使得区块链具有更强的匿名性,但同时使得监管更加困难,同时不能符合法律和法规使得流通性受到限制。在加密货币中使用强匿名性的研究似乎没有意义,但匿名技术的在不同应用场景下使用,效果会大相径庭,基于区块链的身份认证使用隐私保护技术可以很好的实现用户的隐私保护。下面通过对应用于zero cash技术的分析,对您在隐私保护的设计带来一些启发。
区块链隐私保护在非代币的区块链应用,如金融级别企业用户提供高性能、高安全的区块链链上数据隐私保护和隐私数据授权。保障交易数据的端到端,全生命周期的隐私安全。具体的隐私保护体现在对交易执行流程的数据及计算全生命周期保护,如交易数据、合约代码、全局状态数据及交易回执等数据的保护,以及合约执行时的计算过程保护。另外区块链隐私保护在基于区块链的电子贸易平台上对用户的交易数据实现隐私保护,同时对商品的生产和物流实现可追溯性利用通用隐私保护合约链的隐私存证数据流转特性,在保持高性能的同时保护隐私数据流转过程,并借助合约授权能力,使得监管方能够进行全流程监管。此外隐私保护技术在基于区块链的分布式数字身份也有很好的切入点,实现企业在合规性的基础上实现数字身份的创建、验证、管理,实体之间便捷的进行可验证声明的颁发。
二、零知识证明
密码学中,零知识证明[1](zero-knowledge proof)或零知识协议(zero-knowledge protocol)是一方(证明者)向另一方(检验者)证明某命题的方法,特点是过程中除“该命题为真”之事外,不泄露任何信息。因此,可理解成“零泄密证明”。例如,欲向人证明自己拥有某信息,则直接公开该信息即可,但如此方式则会将该信息亦一并泄露;零知识证明的精粹在于,可以证明自己拥有该信息而不必透露信息内容。一个零知识证明系统应该满足:完整性,可靠性,零知识性。
通过NP问题构造零知识证明系统,下面是一个基于离散对数的交互式零知识证明系统,证明者在不泄漏(witness:a)的情况下,让验证者相信自己知道(witness:a).这个交互式证明系统的Σ协议详细过程:

这个方案的witness是一个参数a,另外随机选择一个点a0,对于验证者的询问x可以看成z是在坐标为x处直线上的点,如下图所示。

接着对参数a进行扩展,如果witness是一组参数a1……am,那么就需要通过构造一个多项式实现理想化证明,需要验证者询问m+1次,每次诚实证明者回答的值是多项式对应曲线上的点,如下图所示曲线上的点。

这样就可以实现一个多重离散对数的零知识证明,其中交互过程与上面过程相同,但是参数量会变大,证明和验证的计算量也会变大。详细的过程如下:
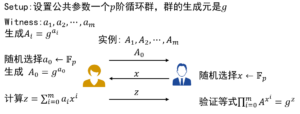
关于非交互式零知识证明的实现,例如在上述方案的基础上,使用Fiat-Shamir启发式,令x=hash(A0,……Am),证明者可以不通过和验证者交互生成一个关于witness的证明,并且任意验证者都可以验证,这个和区块链中任意节点都可以对交易的正确性进行验证相吻合。
三、zk-SNARK
zk-SNARK(Zero-Knowledge Succinct Non-interactive Argument of Knowledge)的特性包含在其名字中,其中有:
- 零知识性(Zero-Knowledge):除了证明实例的真实性外,没有泄漏任何信息给验证者。
- 简洁性(Succinct):证明是简短的,并且可以容易验证(验证者计算量小)
- 非交互式(Non-interactive):不需要上面验证者对x的提问是一次交互,采用Fiat-Shamir启发式即可替换为非交互式。
- 知识的论证(Argument of Knowledge):根据实例生成一个证明,这个证明是计算可靠性下的证明。即只对计算能力有限的证明者有效,如果证明者拥有足够的能力那么就可以伪造证明。
Zerocash中使用的zk-SNARK的技术还是相当复杂,下面基于一个简单的实例描述一个zk-SNARK的方案,同时对zerocash中采用的zk-SNARK的技术点做一个简单介绍。接着上面的多重离散对数零知识证明系统,继续进一步参数进行改变,首先公共参数生成n个生成元 ,并把每一个witness扩展成一个向量,针对验证者的询问x,证明者给出一组z值进行回答,过程如下:

而zerocash使用的zk-SNARK[2]方案中采用了双线性对运算[3],双线性对运算的定义是:

Groth16[2]方案对于多项式的构造:算数电路(Algebraic Circuit) àR1CS(rank-1 constraint system)àQAPàSNARKs的过程其中间转换比较复杂,由于篇幅这里简单的进行概述,对于一个算式可以转换为一个算术电路,针对这个算数电路所有gate转换成R1CS,针对每一个的gate将其转换为a,b,c三个向量,所有gate的a向量组成一个向量组A,同样得到向量组B和C。接着利用拉格朗日插值定理将R1CS形成的3个向量组A、B、C转换成3个多项式A(x),B(x),C(x)其特点是在拉格朗日插值定理恢复这三个多项式时,选择的点必须都相同。这样在这个构造中就可以实现多项式A(x)*B(x)-C(x)的部分解Z(x)=(x-x1)(x-x2)……(x-xn)这些解是利用拉格朗日插值定理恢复多项式时选择的点。所以有等式A(x)*B(x)-C(x)=H(x)*Z(x),并把这些多项式放在指数上构造公共参数和proof,使用双线性对运算验证者验证每一组参数及其组合构成的等式是否成立,如果等式成立验证者相信证明者知道witness。接着还出现了其他简洁式的高效零知识证明方案如Bulletproofs[4]和zk-STARK[5]。
四、Zerocash匿名性的实现
Zerocash一种基于zk-SNARK的匿名数字货币,由2016年11月正式上线以来,除了区块链产业人士外,也得到了学术界的广泛关注。仅通过零知识证明的公开证明信息,就可以实现两个匿名用户之间安全隐私的转账。实现了身份匿名和交易金额保密的一种强匿名性数字货币。具体的实现过程是通过区块链上的交易构造、交易验证、交易接收来实现的。Zerocash的交易分为两种一种是铸币(Mint)另一种是转账交易(Pour)。
4.1 铸币(Mint)
Zerocash的铸币交易过程:用户想把价值为v的比特币转换为ZEC(这里采用1:1兑换)用户首先生成3个随机数r,s,ρ然后通过承诺计算cm和sn,其中cm记录币的生成,而sn记录币的消费,币消费后会记录在sn列表中。其中cm和sn的生成下图所示。
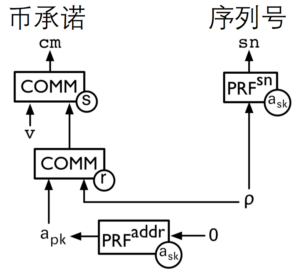
币的铸造
一个ZEC其实是一个向量 (apk,v,r,s, ρ,cm,sn)其中v是ZEC的面值cm记录ZEC的生成,而sn表示ZEC的消费记录,如果sn已经出现在列表中表示此币已经消费,来防止双花。在铸币阶段用户只公布了自己的cm和v,而其他信息只有用户自己知道。
4.2 转账交易
通过上面的铸币交易就可以成功的铸造ZEC,铸造好了ZEC后,下面描述如何花费交易ZEC。下面描述从用户A到用户到用户B的一个交易,用户A拥有的v面额的大零币c,转给用户B的金额为x,给自己找回v-x, 用户A拥有ZEC (apk,v,r,s, ρ,cm,sn) ,向用户B转账的时候需要先询问用户B的地址bpk,,用户A生成两个新币c1,c2。
c1 = (bpk,x,r1,s1, ρ1,cm1)
c2 = (apk,v-x,r2,s2, ρ2,cm2)
其中c1,c2的sn没有生成,只有拥有地址对应的私钥的用户才能生成sn。这也是为什么用户A生成了新币但是不能花费给用户B的原因。并且参数是以加密的形式发送给用户B,用户A不能生成c1对应的序列号sn所以不能花费c1而用户B收到所有的参数,并且拥有bpk对应的私钥生成序列号sn,从而可以花费c1.然后用户A将交易信息公布到区块链网络中TXpour = (sn,cm1,cm2,π),其中π就是零知识证明中生成的proof.用户A将向量(bpk,x,r1,s1, ρ1,cm1)以加密的形式通过端到端的方式传给用户B。下面是zero交易的详细步骤[6]。

五、结论
Zerocash是第一个利用零知识证明zk-SNARK实现了强匿名性的数字货币。不仅实现了对发送方和接收方地址的隐藏,而且实现了隐藏交易金额,仅交易的双发对交易可链接和交易的金额,而其他区块链节点查看的数据只能验证交易的有效性和金额的正确性,但不能得到交易双方和交易金额等其他信息,实现了高等级的强隐私保护。参考零知识证明的应用方法,帮助您在设计身份匿名性和关键数据的隐私保护有启发作用。同时匿名性又是一把双刃剑,对于监管带来极大的困难,所以在匿名性上添加可监管实现可监管下匿名性也是实际应用场景的需求。
参考文献
- Sahai A . Non-Malleable Non-Interactive Zero Knowledge and Adaptive Chosen-Ciphertext Security[C]// Foundations of Computer Science, 1999. 40th Annual Symposium on. IEEE, 1999: 543–553.
- Groth J . On the Size of Pairing-Based Non-interactive Arguments[C]// Annual International Conference on the Theory and Applications of Cryptographic Techniques. Springer, Berlin, Heidelberg, 2016.
- Dan B, Lynn B, Shacham H. Short Signatures from the Weil Pairing[C]// International Conference on the Theory & Application of Cryptology & Information Security: Advances in Cryptology. 2001: 514-532.
- Bunz B , Bootle J , Boneh D , et al. Bulletproofs: Short Proofs for Confidential Transactions and More[C]// 2018:315-334.
- Eli Ben-Sasson, Iddo Ben-Tov, Yinon Horesh, and Michael Riabzev. Scalable, transparent, and post-quantum secure computational integrity. https://eprint.iacr. org/2018/046.pdf, 2018.
- E. Ben Sasson et al., “Zerocash: Decentralized Anonymous Payments from Bitcoin,” 2014 IEEE Symposium on Security and Privacy, 2014, pp. 459-474, doi: 10.1109/SP.2014.36.
上述情形之外的任何使用形式,均需提前向绿盟科技(010-68438880-5462)申请版权授权。如擅自使用,绿盟科技保留追责权利。同时,如因擅自使用博客内容引发法律纠纷,由使用者自行承担全部法律责任,与绿盟科技无关。
